Scenario Strings
During the previous chapters we have assembled a complete model for dealing with MajiroArc archives of both version 1 and version 2. As I have mentioned before, version 2 also features files encrypted with a XOR.
IN this chapter we will learn to decode such files by creating another model to handle MajiroObj files.
The Usual Dump
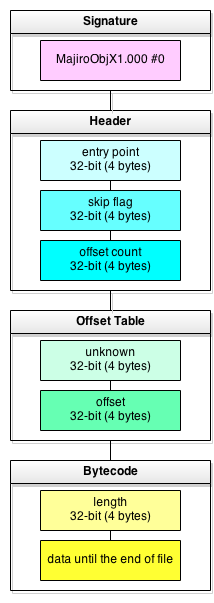
Just like with MajiroArc let’s start with the file structure and a sample hex dump.
0000h: 4D 61 6A 69 72 6F 4F 62 MajiroOb 0008h: 6A 58 31 2E 30 30 30 00 jX1.000. 0010h: 00 00 00 00 54 03 00 00 ....T... 0018h: 01 00 00 00 30 8F 12 1D ....0... 0020h: 00 00 00 00 63 7A 00 00 ....cz.. 0028h: 3A 08 09 00 A0 38 07 77 :... 8.w
- magic signature – this is string «MajiroObjX1.000» followed by a null byte (15+1 bytes in total). Another string, «MajiroObjV1.000» («V» instead of «X») corresponds to the same format but with unencrypted bytecode
- entry point – location of the first instruction opcode that Majiro game engine executes when running this script
- skip flag – some internal engine field; we don’t have to know what it’s for
- offset count – number of Offset Table entries – just like similar fields in MajiroArc
- bytecode length – specifies the size of bytecode – the same as file size minus total size of signature, header, offset table and this field
- bytecode data – stream of instructions that the game engine executes; for example, «show text», «wait for input», «change background», «play music», etc. In ObjX this stream is encrypted, in ObjV it’s raw
Armed with this knowledge we can now write the model. I’m sure that after the last trials it’s a piece of cake for you:
This structure is very straightforward compared to MajiroArc. It has just one cycling table (offsets) and a handful of other 4-byte fields. Everything else is either encrypted (MjArcX) or decrypted (MjArcV) data – bytecode.
Now we have a working model which you can test on this sample and see something like this:
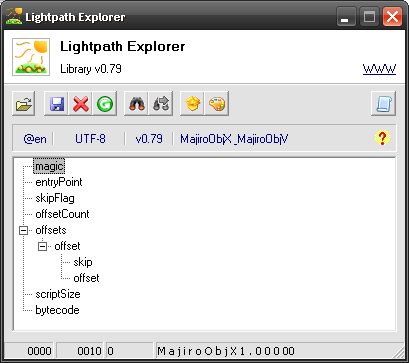
Now we should decode the bytecode node – as you can see on the screenshot it’s an ObjX file recognized by its signature MajiroObjX1.000. This brings us to an exciting subject – cryptography!
Friendly XOR’bits
The word «cryptography» might sound intimidiating to you unless you have a Ph.D in mathematics. However, it’s not necessary all complex. In fact, since the majority of programmers – authors of games and other applications in our area of interest – are ordinary folks just like us they don’t invent their own crypto algorithms for every project they have. Rather, they use some industrial standard – SHA-1 and MD5 are most common. And if it’s industrial it’s very well-known and there are ways to recognize and revert them. They’re also few, which is logical – creating such a standard requires significant effort of many people.
Among Japanese game developers this situation is even better for us. Instead of common cryptographic algorithms they do invent their own – but using just a single technique which is often called XOR, or wind encryption.
As you certainly know computers operate on bits – an atomary value that has just two possible states: one or zero, also called true and false. Bits are also grouped in bytes – 8 bits per byte. Every data is represented by a stream of bytes.
A bit is very «small» unit of information – if it was a number we could only represent 0 and 1. However, we can make numbers of arbitrary length by combining bits together. Ket’s take one byte (8 bits):
11111111
These are 8 bits, each having the state of true (digit 1). Using a simple formula we can calculate the amount of all possible values a byte can have:
2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 = pow(2, 8) = 256
So a byte can hold up to 256 values. Much better than just a bit!
Since computers operate on bits, which are numbers, characters are also represented as numbers. A symbol is assigned – mapped to – a certain digit – and tables of such assignments are called character sets (charsets) or code pages (CP). Examples of charsets are Windows-1251, KOI8-R and various flavors of Unicode.
Usually most charsets have the same codes for Latin letters and many other common symbols like colon, space, dash, digits and others. For example, string magic can be encoded as the following set of bytes (you can use resources like asciitable.com for character table lookups):
+-----+-----+-----+-----+-----+ | m | a | g | i | c | +-----+-----+-----+-----+-----+ | 109 | 97 | 103 | 105 | 99 | +-----+-----+-----+-----+-----+
In hexadecimal notation that we’ve already seen in hex dumps this string has the following form:
6D 61 67 69 63
In mathematics there are operators like addition, subtraction, multiplication and division. In binary mathematics there also are operators – called bit-wise since they operate on bits. Sometimes they’re also called «logic» operators as they operate on true/false values. Such operators include NOT, AND, OR and XOR. Let’s see how they work.
For example, number 109, which is the code of letter «m», in binary notation – i.e. written with only ones and zeroes – look like this: 1101101.
NOT operation flips every bit. If we apply it to letter «m»:
6D = 1101101 NOT = 0010010
This is number 18 in decimal notation and 12 in hexadecimal. Not really a code of any character.
AND operation produces one if both bits are one and zero in all other cases. If we apply it to letters «m» and «g»:
6D = 1101101 61 = 1100111 AND = 1100101
This is number 101, hexadecimal 65 – letter «e». Funny binary world!
OR operation is somewhat similar to AND but produces zero only if both bits are zero. If we apply it to letters «m» and «g»:
6D = 1101101 61 = 1100111 OR = 1101111
This is number 111, hexadecimal 6F – letter «o».
Finally, most interesting operator XOR has more complex logics and the following table will help us understand:
+---+---+--------+ | A | B | RESULT | +---+---+--------+ | 0 | 0 | 0 | | 0 | 1 | 1 | | 1 | 0 | 1 | | 1 | 1 | 0 | +---+---+--------+
In other words, XOR produces zero if both bits are the same and one if they are different. This is the single most used operation in «amateur» cryptography – although not amateurs actively use it too but combine with many other calculations. Let me show why it’s so useful.
Let’s apply XOR to letters «m» and «g»:
6D = 1101101 61 = 1100111 XOR = 0001010
Bitwise operations are commutative meaning that the order of operands doesn’t matter. We could apply NOT, AND, OR and XOR to letters «g» and «m» and still get the same result.
Ths is number 10, hexadecimal A. Not a letter. However, let’s apply this number to «g»:
0A = 0001010 61 = 1100111 XOR = 1101101
Let me check… whoa, it’s letter «m»! Can it be a coinscidence? Let’s XOR «a» and «i»:
61 = 1100001 69 = 1101001 XOR = 0001000
Number 8. Let’s XOR it and «a»:
08 = 0001000 69 = 1101001 XOR = 1100001
Letter «i»! What if we XOR 8 and «i»?
08 = 0001000 61 = 1100001 XOR = 1101001
It turns out that XOR works «round-way»: if we have 2 operands and the result of XOR’ring them then applying that result to either of the operands will produce the other operand. This is perfect for concealing information without too much computation trouble.
The following is word «magic» spelled in binary notation:
1101101 1100001 1100111 1101001 1100011
Now let’s secretly agree that we are going to use letter «K» as our key to first conceal and then reveal our data. This letter’s code is 75, hexadecimal 4B, binary 1001011. Let’s XOR it with «magic»:
magic = 1101101 1100001 1100111 1101001 1100011 KKKKK = 1001011 1001011 1001011 1001011 1001011 XOR = 0100110 0101010 0101100 0100010 0101000 dec = 38 42 44 34 40
If we look up these decimal numbers in a character table we will get the following string: &*,"( – meaningless but even better for our conspiracy!
Now suppose you get a piece of paper, write down that string and call up Joe. When he comes you instruct him to bring this precious piece of data to me. The best part here is that even if Joe realizes how secret the message is he can’t make any sense from that paper. However, when I see this note I ponder for a second and then recall that we’ve agreed to use letter «K» as the key to our little secrets. So I take a pencil and scribble down the following simple calculation:
&*,"( = 0100110 0101010 0101100 0100010 0101000 KKKKK = 1001011 1001011 1001011 1001011 1001011 XOR = 1101101 1100001 1100111 1101001 1100011
But our schizophrenia fantasy doesn’t end there. After all, if Joe was careless enough to have lost the note it would take just 256 calculations for a bad guy to eventually decrypt our message. What if we use another string – let’s say «KEY» – to code our message? This way:
magic = 1101101 1100001 1100111 1101001 1100011 KEYKE = 1001011 1000101 1011001 1000101 1001011 XOR = 0100110 0100100 0101100 0101100 0101000 dec = 38 36 44 44 40
Another meaningless string: &$,,(. Interestingly, this time we’ve got two identical symbols in place of «g» and «i» even though our original string has different letters there. As you see it all depends on the key used to XOR the original data. Cryptographic algorithms like this one are called symmetric – if you first apply XOR to data you will get crypted version but if you apply the same XOR to crypted data you will get original version.
Now no matter how reckless Joe is no bad guy will be able to crack our secret code. After all, even if he knows the length of our key it is 256 * 256 * 256 – 16777216 possible values! No way he’ll be able to calculate this by hand. Mission clear!
I’m obviously bending the facts here. Cracking of keys doesn’t have to be so blunt; often we have assumptions about either original data, key or both – such as range of values (characters), length, kind of data – for example, textual data might take 1/3 or ½ of full byte range so it’s not 256 but less than 100 values per byte which is already 10 times less. Even more, with the power of today’s computers – or many computers combined in a computation network – it’s possible to pick up millions of combinations with complex computations per second so our little secret has no chance to stand for long.
Byte value 0 doesn’t crypt input data so XOR’ing with it will always yield the original value: 11 xor 00 = 11. Generally, the fewer bits with value of 1 the key has the less it will mangle the data.
Xobjects
I hope you’ve enjoyed our short journey into the world of cryptography. Now we can get back to decrypting MajiroObj scenarios and in particular their ObjX version. From my earlier studying of this game engine I’ve learned that it uses a 1024-byte string to XOR data with. Here it is (the same file found in the archive with sample.mjo).
If we take every byte in bytecode and XOR it with every byte in this string we will get encoded data. However, it doesn’t look doable – plus we don’t want to do this for every script we have got – which are sometimes hundreds in one game.
And of course we don’t have to. There’s an easy way and we’ll once again use Lightpath expressions to transform encoded data into decoded bytecode.  Modell the sample scenario with the model we’ve created above and check Node Properties of bytecode node. You will see that it starts at 2B and ends at 7A8B, being 31331 bytes long. This is what scriptSize tells us as well.
Modell the sample scenario with the model we’ve created above and check Node Properties of bytecode node. You will see that it starts at 2B and ends at 7A8B, being 31331 bytes long. This is what scriptSize tells us as well.
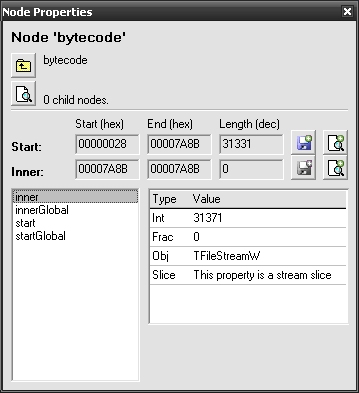
Click  Save on the right of Start line to save the encrypted version of bytecode. Now use the same button but this time with a
Save on the right of Start line to save the encrypted version of bytecode. Now use the same button but this time with a  right-click. You will be prompted for an expression string to transform the data with. Enter the following:
right-click. You will be prompted for an expression string to transform the data with. Enter the following:
'mjobj.xor' load h2b xor
Provided that you have mjobj.xor file in the same directory as sample.mjo you will instantly get an unencrypted version of the same bytecode. It’s easy to check – just open it and the encoded version in any hex editor such as 010 Editor and compare with a quick glance. Scroll down the file and you will see what looks like regular lines of text: black450, bg04a0, st00_a00, v00tr0028 and other strings. Their presense and presense of zero (00) bytes is usually the first sign of «real» data while absense of both indicates that the data has been tampered with.
The expression we have used above stands for the following:
- 'mjobj.xor'
- A string constant – name of file that holds the hexadecimal sequence of bytes used to XOR crypted bytecode with.
- load
- This function loads string from disk and pushes it onto the RPN stack. It takes one parameter off – the name of file – and puts back the data it’s read.
- h2b
- This is «hex-to-binary» function that converts hexadecimal string into raw bytes. We could have avoided this function if only MajiroObj didn’t use codes that don’t correspond to letters (00, 07 and others). Because of this we have to have a hex dump in our mjobj.xor which is converted into «real» values by this function.
- xor
- The actual XOR function. Applies XOR to every byte in the first parameter by using second parameter as the key string. Once again, we could have avoided the entire row of functions before this one by writing just 'MySecretKey' xor – however, MajiroObj’s key is too long to fit in our expression.
Le PaXor
Now we can create our second lpx build – decoding MajiroObjX scripts and encoding MajiroObjV. Our Options section would look like this:
lp== Options == lpx.DataPath = bytecode$start lpx.DataExpr = 'mjobj.xor' load h2b xor lpx.DefaultFiles = *.mjo
However, it still feels a bit rough. With this our custom lpx build would have to come with mjobj.xor file or extraction (de/encoding) would fail. lpx extends the load function in a way that allows us read arbitrary section from our Lightpath script. For this we simply need to replace path to file with a string like this:
:Section Name:Subsection Name
Both section’s and subsection’s names are optional, as well as colon before the latter. Here are some examples:
- : – just a colon will read script’s preamble – text between the first script line (signature) and the first section.
- :My Section – Reads contents of the unnamed subsection of section My Section. «Unnamed» means the subsection between == My Section == and the first === Subsection === inside it.
- :My Section: – the same as above.
- :My Section:Sub Section – reads contents of subsection Sub Section from My Section.
If we had this script then numbers in brackets correspond to examples above:
lpLightpath 0.79 (1) Preamble. == My Section == (2) (3) Unnamed contents. === Sub Section === (4) Subsection contents.
With this we can easily transfer mjobj.xor contents under any section and use it to encode the bytecode. Below is the complete MajiroObj model that is ready to go with lpx:
If you embed it with
shlpx ! MajiroObj.lp, put the new program into the directory with sample.mjo and run it you will see a new folder with a single file inside – this is our decrypted bytecode. Since we didn’t specify any lpx.NamePath lpx has generated an automatic file name which is unique to that particular model/file combination.
You can also add MajiroArc support to the same lpx build with
shMajiroObj.exe !+ MajiroArc.lp – note the plus sign (+) following the exclamation mark (!) – it tells lpx not to remove existing models but only add the new one. With this single build you will be able to extract MajiroArc of both versions and decode MajiroObjX as well.
Stringrabs
This is a bonus section to give you yet another idea of when Lightpath might be useful. We now have the decoded version of Majiro scenario files. As I’ve mentioned above, scenarios are «programs» that the Majiro game engine executes – very much like regular Windows or *nix executables built for real CPUs. Scenarios have their own «assembly language» to code different operations – like «show text».
With a quick look over the decoded bytecode we will notice a lot of strings popping up here and there:
0110h: 25 00 00 08 E8 03 00 00 01 08 09 00 73 74 30 30 %...è.......st00 0120h: 5F 61 30 30 00 10 08 9C BF 34 3C 00 00 00 00 02 _a00...œ¿4<..... 0130h: 00 3A 08 26 00 10 08 74 1E 27 5F 00 00 00 00 00 .:.&...t.'_..... 0140h: 00 01 08 0A 00 76 30 30 74 72 30 30 32 38 00 10 .....v00tr0028.. 0150h: 08 F0 FD 2A 81 00 00 00 00 01 00 3A 08 27 00 40 .ðý*.......:.'.@ 0160h: 08 39 00 91 CC 83 41 83 93 81 75 82 60 82 62 82 .9.‘̃Aƒ“.u‚`‚b‚ 0170h: 75 82 CD 81 41 83 41 83 69 83 55 81 5B 81 45 83 u‚Í.AƒAƒiƒU.[.Eƒ 0180h: 4C 83 83 83 89 83 4E 83 5E 81 5B 81 45 83 72 83 Lƒƒƒ‰ƒNƒ^.[.Eƒrƒ 0190h: 85 81 5B 82 CC 97 AA 82 CB 81 76 00 41 08 10 08 ….[‚Ì—ª‚Ë.v.A...
Actual strings are marked with yellow; apart from them we also have string lengths and terminating null byte.
You might wonder why I have highlighted last 4 lines as a string because it seemingly contains just garbage. However, to my trained eye it looks like a Shift-JIS-encoded string which we can indeed confirm by copy-pasting it into a blank text file and opening in a Shift-JIS-capable editor like Notepad2.
Shift-JIS strings are used to encode Japanese texts with every character typically being encoded as 2 bytes with first byte in range above 80 (hexadecimal). Here we indeed see 91, 83, 82 and others (underlined in the hex dump above).
String lengths are 16-bit (2 bytes) numeric values that specify the number of bytes starting from the string’s first character end up until its last character, plus one for terminating null byte (00).
Why we might be interested in all this info on strings? Well, it’s extremely useful if we decide to do a fan translation of a game powered by Majiro engine. With official translations when a company buys license and right to translate and sell the translated game it also receives all the tools necessary to reassemble game data with new texts. However, fan translations are unofficial, they don’t have official tools available and thus rely on the work of hackers – regular fellows just like you and me – who decipher the format of game data files and create tools to first extract strings into some common text file format (omst often .txt) and then put these strings back into the game.
Lightpath can’t help you replace these strings but it can help you quickly prototype the extractor. This is what we’re going to do below.
As far as we’ve found out strings have these format:
LL LL CC CC CC CC ... 00
…where LL LL stands for 16-bit string length, CC ... – for string symbols and 00 – for terminating null byte.
We now can write a very quick and dirty string extractor model:
You should be able to unerstand what’s going on here so just let me give you a few tips:
- Since we don’t know exactly where a string will start we are using tentative context marked with circumflex (^) to ignore any errors it generates since they indicate that it’s not a string we’re trying to grab at this position.
- If str context fails we simply skip this byte with % ANY.
- In this model len (string length) is treated as a single byte rather than 2 bytes. This is so to lower false positives – after all, most strings will have less than 254 (255 – 1 for null byte) bytes, or 122 symbols in Shift-JIS.
- chars’ condition serves the same purpose: to eliminate noise from the output – we’re not interested in strings below 2 Japanese/4 Latin symbols.
- [^\0-\31] is a Simpat expression that matches range of characters not (^) having codes (as indicated with leading slash in front of digits) from 0 to 31 – these are called «control characters» and are not normally present in strings. With this check we reduce false positives. Note though that with this we also eliminate line breaks which have codes of 10 and 13.
If you apply this model to the decoded bytecode of our sample you will see several hundreds of strings which you can  Extract as usual. You will also have to wait a dozen of seconds – maybe up to a minute – until Lexplore processes the file. This is unsuitable for real world tool and eventually we would want to write our own script extractor in another language like C or Delphi but by that time we will have complete knowledge of the data format thanks to Lightpath. Doing this kind of research without a modeller would normally require much more time and effort before we can fully understand the data.
Extract as usual. You will also have to wait a dozen of seconds – maybe up to a minute – until Lexplore processes the file. This is unsuitable for real world tool and eventually we would want to write our own script extractor in another language like C or Delphi but by that time we will have complete knowledge of the data format thanks to Lightpath. Doing this kind of research without a modeller would normally require much more time and effort before we can fully understand the data.